Критерий устойчивости Найквиста-Михайлова

Он позволяет определить устойчивость замкнутой системы по виду АФЧХ системы в разомкнутом состоянии. Различают формулировка критерия для случаев, когда система в разомкнутом состоянии устойчива и неустойчива. В первом случае критерий устойчивости формулируются так: САУ, которая устойчива в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если АФЧХ разомкнутой системы не охватывает точку на комплексной плоскости с координатами (-1, j0).

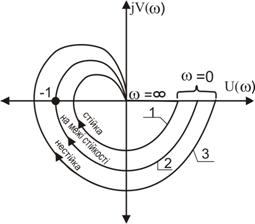
На рис.1.1 показаны АФЧХ статических систем: с пометкой 1 — для устойчивых систем, 2 — на грани устойчивости, 3 — неустойчивых систем. АФЧХ статических систем начинаются с положительной полуоси при = 0, а заканчивается в начале координат при = 0.

Рис 1.1 АФЧХ статических систем.

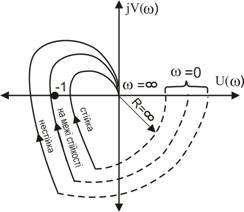
На рис.1.2 показаны АФЧХ астатическим систем.

Рис 1.2 АФЧХ астатическим систем

Потому что характеристическое уравнение таких разомкнутых САУ не имеет членов свободных от «p» [например для разомкнутой САУ рис.1.3 характеристическое уравнение: р (Т1р +1) (Т2р +1) = 0], то АФЧХ при = 0 достигает в бесконечность. Замыкание АФЧХ с положительной действительной полуосью в этом случае осуществляется дугой нескончаемого радиуса, как показано на рис.8.6
Физическое значение амплитудно-фазового критерия возможно объяснить так: сигнал на выходе разомкнутой САУ всегда опаздывает по фазе от входного, так как в состав САУ входят апериодические, интегрирующие, колебательные и прочие звенья, которые вносят опоздание колебаний по фазе. И это опоздание увеличивается с ростом частоты./p>

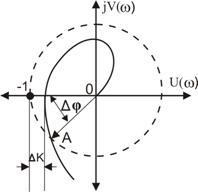
Рис 1.3 Запасы устойчивости.

Тогда запасы стойкости:

• По амплитуде-ΔК, это та величина, на которую еще надо увеличить коэффициент передачи системы, чтобы она достигла предела устойчивости;
• По фазе-Δφ, это тот угол, на сколько сдвиг по фазе не достигает критического угла (-1800), когда система становится неустойчивой.

Вообще замкнутая САУ может быть устойчивой и тогда, когда разомкнутая система неустойчива. В этом случае этот критерий имеет более общую формулировку: САУ, которая нестойкая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если АФЧХ разомкнутой САУ охватывает критическую точку (-1, j0) в положительном (положительном) направлении раз, где m — число корней характеристического уравнения разомкнутой системы, лежащие в правой на полуплоскости.

Этот критерий особенно интересен тем, что не требует знания уравнения или передаточной функции системы. Надо иметь лишь АФЧХ разомкнутой системы, которая может быть получена и экспериментально, что во многих случаях точнее и надежнее.